|
2. 最小二乗法によるパラメータ同定
一般に，パラメータを同定するためには，ロボットを動かし得られた関節角度，角速度，角加速度とトルクのデータから
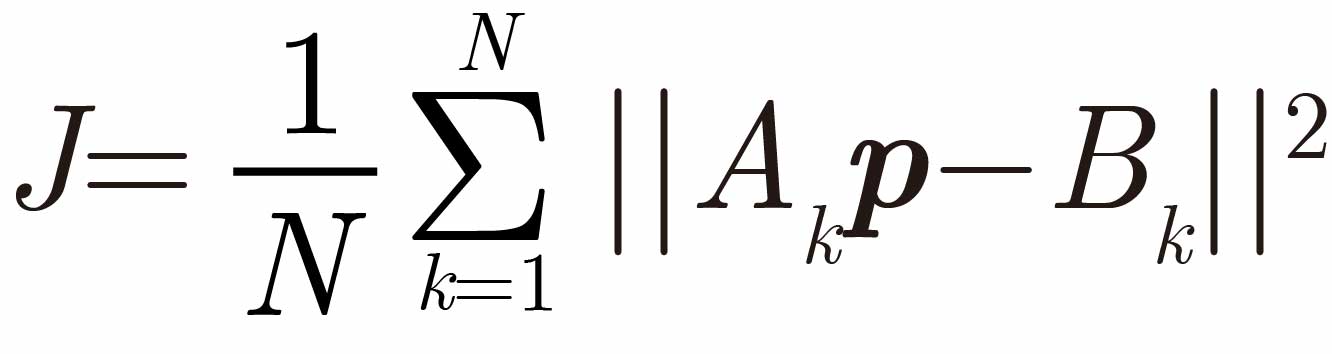
を最小化するpを最小二乗法によって求めます．しかし，これは運動方程式の左辺と右辺の差の最小化であり，pがどのような誤差を持っているかを評価できません．
|
3. 確率的パラメータ同定
そこで，本研究では運動方程式は常に満たされる，満たされない誤差は最小動力学パラメータが確率的に変動しているからである，と考え，運動方程式を
まず，与えた軌道を媒介変数を用いて関数近似します．
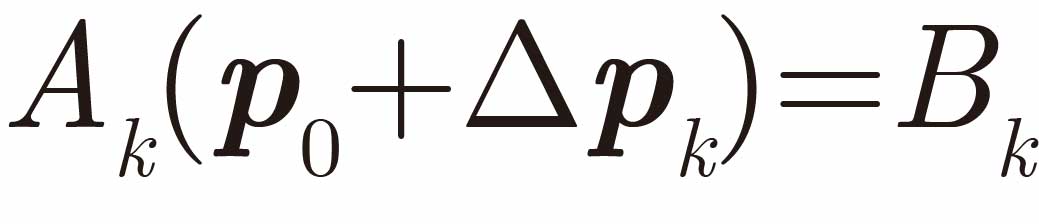
とみなします．これにより，次式が導かれます．
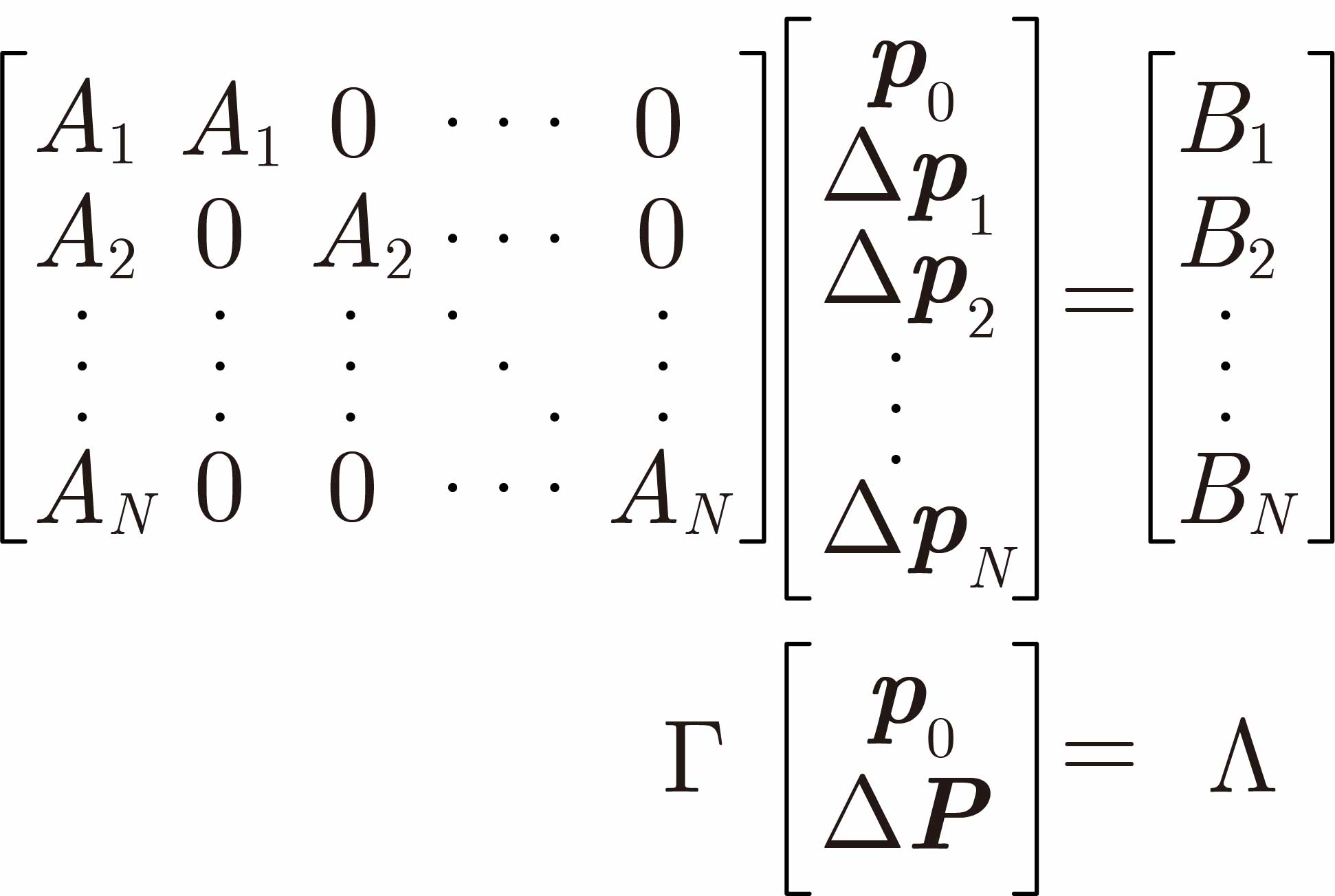
この結果から，最小動力学パラメータとその誤差は，自由パラメータを用いて
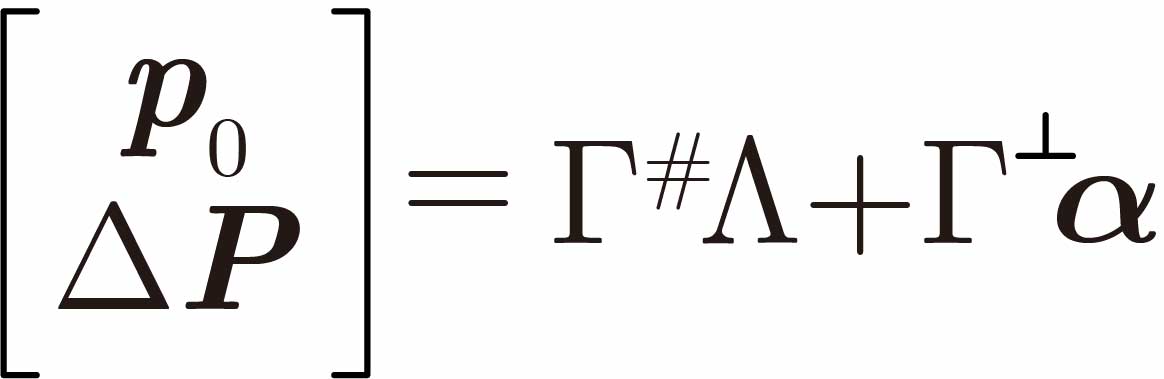
で表されます．そこで，パラメータ誤差が所望の自己共分散
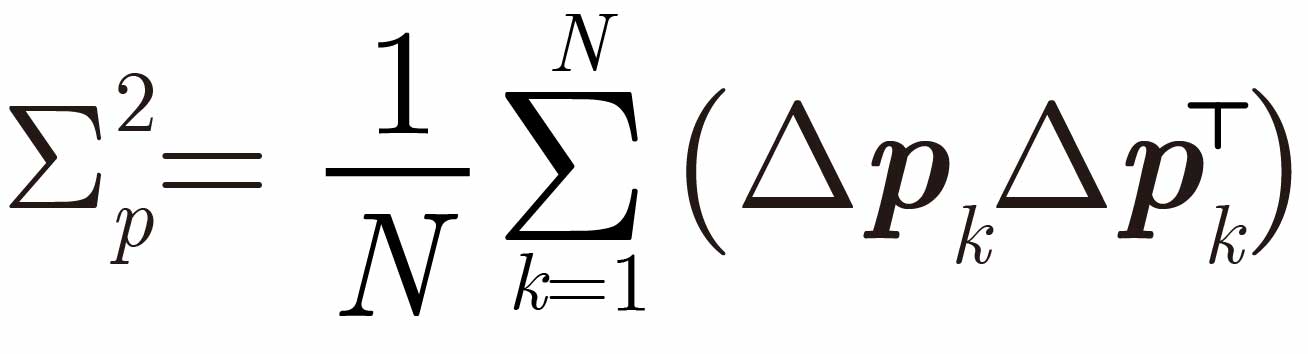
を持つように自由パラメータを求めます．
|
|
4. 感度解析
ここでは，ロボットの手先位置のパラメータに関する感度からパラメータ誤差の自己共分散を指定します．これにより，ロボットにある運動をさせたときの手先位置誤差に大きな影響を与えるパラメータは正確に，そうでないパラメータは粗くても良いようにパラメータ同定ができます．
これを平面3リンクマニピュレータの周期運動に適用して検証しています．
 |
e-mail :  .m.aa@m.titech.ac.jp
| 
